The Indian Railways is currently conducting the recruitment process for 18,799 Assistant Loco Pilot (ALP) positions. The examination for this recruitment process will be held from 25th November to 29th November 2024. The Quantitative Aptitude section is a crucial part of the RRB ALP exam, with 20 out of 75 questions are asked from this section. To assist the candidates in their preparation, we are providing Quantitative Aptitude questions for the RRB ALP exam, along with their solutions. By practicing these questions, the candidates can enhance their skills and increase their chances of cracking the RRB ALP examination in their very first attempt.
Quantitative Aptitude Questions for RRB ALP with Solutions
The Quantitative Aptitude section covers a wide range of topics, and mastering these concepts can greatly contribute to the candidates’ overall performance in the exam. We encourage all the aspiring candidates to thoroughly practice these questions and familiarize themselves with the exam pattern and the type of questions asked. It is crucial for the candidates appearing for this exam to have a strong preparation in the Quantitative Aptitude section to ensure their success.
Q1.
![]()
(a) 2
(b) 4
(c) 1
(d)0
Q2.
![]()
(a) 5/7
(b) 1
(c) 4/3
(d)2/3
Q3. If a + b = 9, ab = –7 then a³ + b³=?
(a) 833
(b) –244
(c) 918
(d) –833
Q4. If roots of a² + 6a + x = 0 are equal then x =?
(a) –3
(b) 3
(c) √3
(d) 9
Q5.
![]()
(a) 0
(b) –1
(c) 2
(d) 1
Q6. x + y + z = 6 and xy + yz + zx = 11, Then what is the value x³ + y³ + z³ –3xyz = ?
(a) 18
(b) 54
(c) 36
(d) 66
Q7. If x + y = 8, then what is the value of x³ + y³ + 24xy?
(a) 40
(b) 512
(c) 64
(d) 8
Q8.
![]()
(a) 18
(b) 34
(c) 16
(d) 14
Q9. If x + y + z = 12, xyz = 3, and xy + yz + zx = 14. Find x³ + y³ + z³.
(a) 1233
(b) 1431
(c) 1369
(d) 1562
Q10. If a² + b² = 3 and c² + d² = 4, then the value of (ad – bc)² + (ac + bd)² is
(a) 3
(b) 12
(c) 5/9
(d) 4/7
Q11.
![]()
(a) 3
(b) 2
(c) 4
(d) 5
Q12.
![]()
(a) 4/9
(b) ½
(c) 1
(d) 2
Q13.
![]()
(a) 5
(b) 15
(c) 7
(d) 17
Q14.
![]()
(a) 0
(b) 1
(c) -1
(d) 2
Q15.
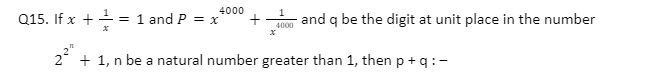
(a) 4
(b) 6
(c) 8
(d) none of these
Solutions:
S1. Ans.(a)
Sol.
a=1
b=-1
c=0
![]()
S2. Ans.(b)
S3. Ans.(c)
Sol.
(a +b)² = a² + b² + 2ab
81 = a² + b² – 14.
a² + b² = 95
a³ + b³ = (a + b) (a² + b² – ab)
= 9× (95 + 7)
= 918
S4. Ans.(d)
Sol. By options
a² – 6a + x = 0
(a -b)² = a² + b² – 2ab.
(a – 3)² = a² + 9 –6a.
Here x = 9.
S5. Ans.(c)
Sol.
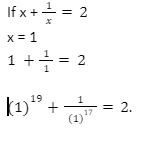
S6. Ans.(a)
Sol.
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² –xy – zx – zy)
= 6(36 – 33)
= 18
S7. Ans.(b)
Sol. (x + y)³ = x³ + y³ + 3xy (x + y)
(8)³ = x³ + y³ + 3xy (8)
512 = x³ + y³ + 24xy
S8. Ans.(b)
Sol.
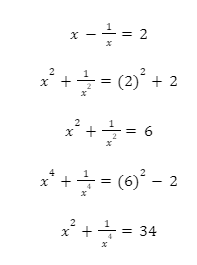
S9. Ans.(a)
Sol.
x³ + y³ + z³ = (12) {(12)2-3(14)}+9
= 12 (144 –42) + 9
= 12 (102) + 9
= 1233
S10. Ans(b)
Sol.
(ad – bc)² + (ac + bd)²
(ad)² + (bc)² – 2(ad)(bc) + (ac)² + (bd)² + 2(ac)(bd)
a²d² + b²c² – 2abcd + a²c² + b²d² + 2abcd
d²(a² + b²) + c²(a² + b²)
(a² + b²) (c² + d²) = 3 × 4 = 12
S11. Ans(d)
Sol.
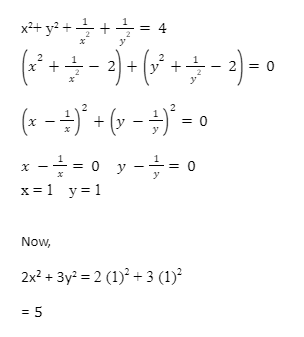
S12. Ans. (d)
Sol.
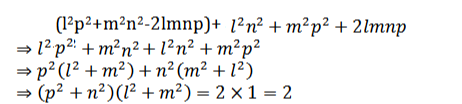
S13. Ans. (a)
Sol.
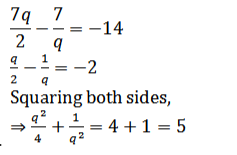
S14. Ans. (a)
Sol.
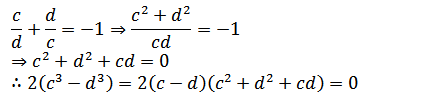
S15. Ans.(b)
Sol.
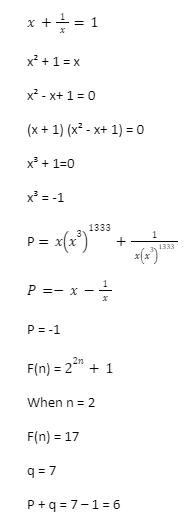



 One Lakh Posts Vacant in Central Armed P...
One Lakh Posts Vacant in Central Armed P...
 CM Announces 10 Lakh Additional Vacancie...
CM Announces 10 Lakh Additional Vacancie...
 Bihar Govt Announced 2.11 Lakh Vacancies...
Bihar Govt Announced 2.11 Lakh Vacancies...


