Area Of Trapezium: Definition, Properties, Formula And Examples

A trapezium is a four-sided shape with one set of parallel sides. The parallel sides are called the bases of the trapezium, and the non-parallel sides are called the legs. The altitude of a trapezium is the perpendicular distance between the bases. The area of a trapezium is equal to the average of the bases multiplied by the altitude.

Trapeziums are a common shape in nature and in everyday life. For example, the wings of a butterfly, the roof of a house, and the teeth of a saw are all trapeziums. Trapeziums are also used in many different structures and machines, such as bridges, airplanes, and cars.

Area of Trapezium

A trapezium is a 2D figure, it is a quadrilateral and has 4 sides out of which 2 sides are parallel to each other. The area of a trapezium is equal to the sum of the areas of the two triangles and the area of the rectangle. A trapezium where the two parallel sides are equal and form equal angles at one of the bases is called the isosceles trapezium.

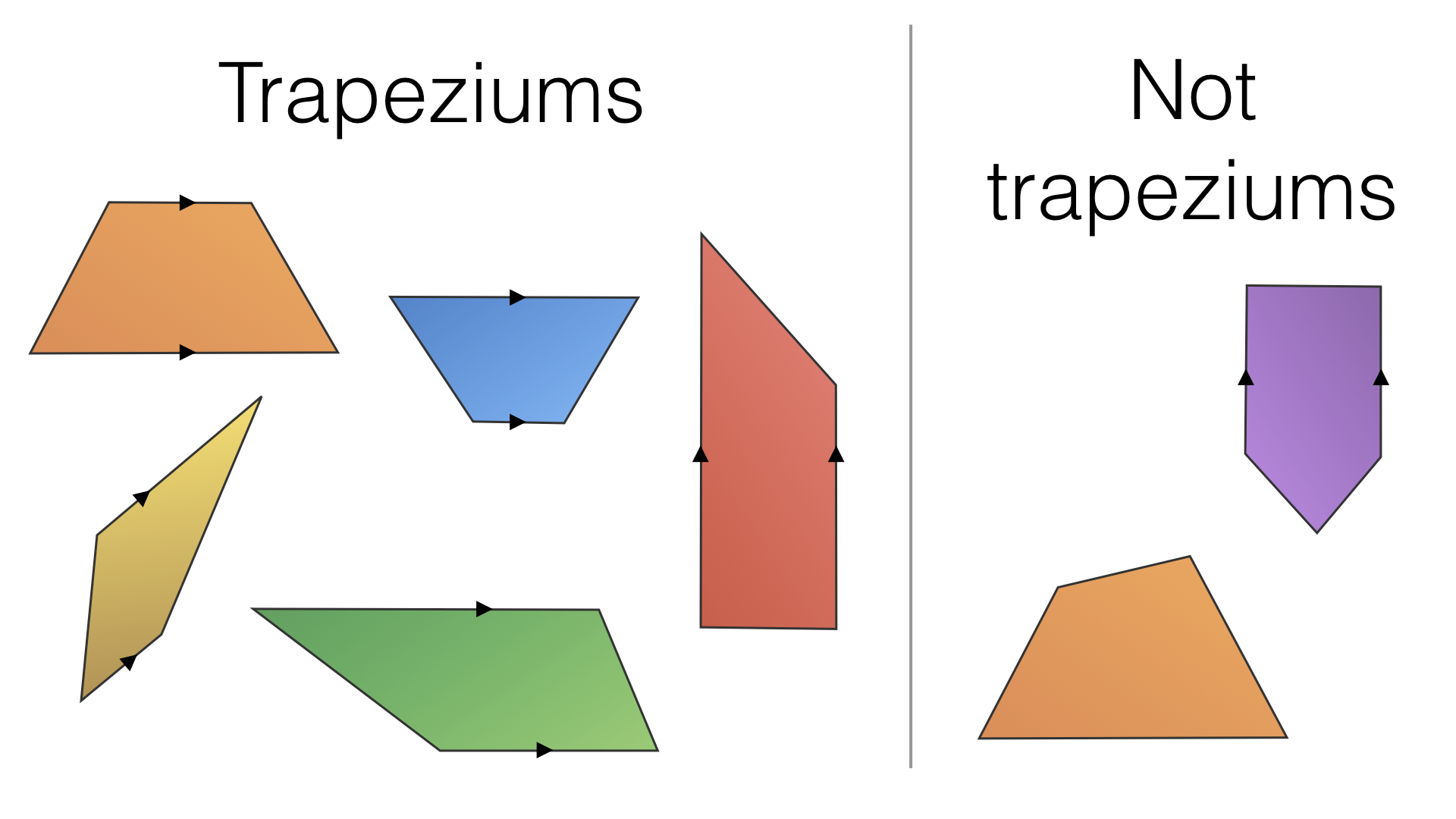
Properties of Area of Trapezium

Some of the properties of a trapezium are listed below:

1. The sum of the angles of a trapezium is 360º
2. A trapezium is not a parallelogram (as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram).
3. The 4 sides of a trapezium are unequal unless it is an isosceles trapezium in which the 2 parallel sides are equal.
4. The diagonals of a trapezium bisect each other.
5. Two pairs of adjacent angles of a trapezium sum up to 180 degrees.

The formula of the Area of Trapezium

In order to calculate the area of a trapezium, you need to draw a perpendicular between the two parallel lines. The perpendicular will be donated as the height ‘h’ which is the distance between the parallel sides.

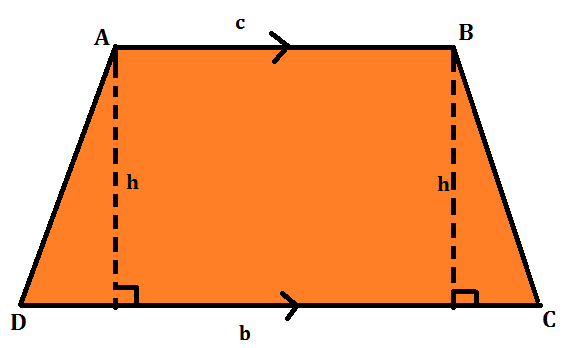
Hence, the area of a trapezium is given by the formula:

Area of Trapezium = 1/2 x distance between the parallel sides x Sum of parallel sides

Area = 1/2 x h x (AB + DC)

Area of Trapezium Examples

Q1: The length of the two parallel sides of a trapezium are given in the ratio 3: 2 and the distance between them is 8 cm. If the area of trapezium is 400 cm², find the length of the parallel sides.

Solution: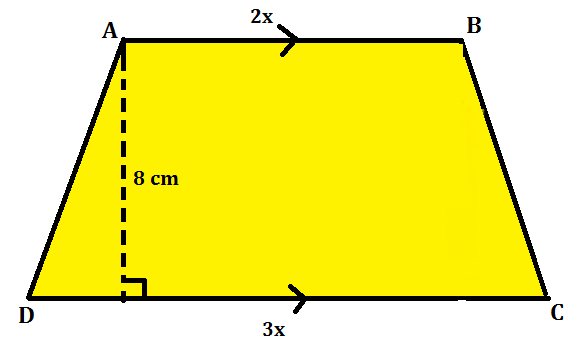

Let the 2 parallel sides as 3x and 2x.

Then, as the area of trapezium is 1/2 x distance between the parallel sides x Sum of parallel sides.

400= 1/2 x (3x + 2x) x 8

400 = 1/2 x 5x x 8

400 = 20x => x = 20 cm

The length of the parallel sides are 60 cm and 40 cm.

Q2. Two parallel sides of a trapezium are of lengths 27 cm and 19 cm respectively, and the distance between them is 14 cm. Find the area of the trapezium.

Solution:

Area of the trapezium = ¹/₂ × (sum of parallel sides) × (distance between them)

Area of the trapezium = {¹/₂ × (27 + 19) × 14} cm² = 322 cm²

Q3. The area of a trapezium is 352 cm² and the distance between its parallel sides is 16 cm. If one of the parallel sides is of length 25 cm, find the length of the other.

Solution: 

Let the length of the required side be x cm.

Then, area of the trapezium = {¹/₂ × (25 + x) × 16} cm²

Area of the trapezium = (200 + 8x) cm².

But, the area of the trapezium = 352 cm² (given)

Therefore, 200 + 8x = 352

                ⇒ 8x = (352 – 200)

⇒ 8x = 152

⇒ x = (152/8)

⇒ x = 19.

The length of the other side is 19 cm.